浙江省考四种方法解排列组合题
排列组合是数量关系中常见考点之一，也是大家难以攻破的考点之一。排列组合问题本质上是计数问题，即计的是方法数和结果数。排列组合的计算可以有多个维度和切入点，而不同的切入点难易层度不同，若能快速找到简单的切入点，则能快准狠地解题。
排列组合题常用到以下四种解题方法：
1、优限法
元素对位置有要求或者位置对元素有要求时，优先安排有绝对限制条件的元素或者位置。
2、捆绑法
元素要求相邻时，先将需要相邻的元素捆绑成一个整体，与其他元素一起进行排序，再考虑捆绑的内部元素是否需要排序。
3、插空法
元素要求不相邻时，先将其他元素排好，再将不相邻的元素插入已排好的元素形成的满足条件的空隙中(注意首尾位置是否满足要求)。
4、间接法
如果题目直接考虑需要分类比较多，而它的对立面包含情况比较少方便计算，我们可以用总方法数减去对立面方法数进行计算。
【小测验】
【例1】五名优秀组员按顺序做年终总结报告，小张只能第一个或最后一个作报告，一共有多少种报告顺序？
A.24
B.36
C.48
D.60
答案：C
【解析】分析题目，其中对于小张而言，有绝对的位置限制，那么这道题应该采用优限法来解题，要优先考虑小张的位置。由于小张只能第一个或最后一个作报告，那他只能从这两个位置中选一个，有2种选择方法。对于其他人而言，题目没有任何限制，那剩余的4人可以任意选择报告位置，有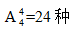
选择方法，所以共2×24=48种报告顺序，结合选项，答案就是C。
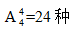选择方法，所以共2×24=48种报告顺序，结合选项，答案就是C。 【例2】五名优秀组员按顺序做年终总结报告，同部门的小张和小李顺序相邻，一共有多少种报告方式？
A.24
B.36
C.48
D.60
答案：C
【解析】分析题目，小张和小李相邻作报告，所以这道题应该采用捆绑法来解答。假设将小张与小李捆绑在一起，则小张与小李作报告顺序一定相邻。将小张和小李看作一个整体，与剩余三人进行排序，共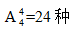报告顺序，但是小张与小李两个人之间也要排序，共2种报告顺序。所以一共有24×2=48种报告顺序，所以答案选C。
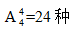报告顺序，但是小张与小李两个人之间也要排序，共2种报告顺序。所以一共有24×2=48种报告顺序，所以答案选C。 【例3】五名优秀组员按顺序做年终总结报告，同部门的小张和小李顺序不能相邻，一共有多少种报告顺序？
A.64
B.72
C.86
D.98
答案：B
【解析】分析题目，小张和小李不相邻，所以这道题应该采用插空法来解答。插空法的使用原则是先将没有要求的人的顺序排好，再将小张和小李插入这些人形成的空隙中，则小张和小李自然不相邻。根据这个方法，除小张与小李外，还有3个人，3个人排序方法有3个人形成了4个空位，再从4个空位中选两个出来让小明和小红去插入，有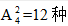
顺序，则总的报告顺序有6×12=72种。故答案选B。
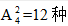顺序，则总的报告顺序有6×12=72种。故答案选B。 【例4】某交警大队的16名民警中，男性为10人。现要选4人进行夜间巡逻工作，要求男性民警不得少于2人，问：有多少种选人方法？
A.1605
B.1520
C.1071
D.930
答案：A
【解析】男性民警为10人，则女性民警有6人。现要选四人且男性民警不得少于两人，所以采用间接法，则男民警可以有2人、3人、4人，这三类情况，情况数较多，考虑对立面，男性民警少于2人，即没有男性民警或只有1名男性民警，两类情况，所以我们可以用总的情况数-1男3女的情况数-0男4女的情况数求解，则本题所求为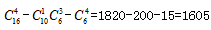
种。故本题选A。
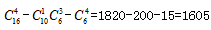种。故本题选A。
点击分享此信息：
相关文章
