利用比较构造法解方程题
在做行测数量关系题目时,有相当一部分的题目是需要寻找等量关系建立方程进行求解,说到方程,想必大家第一反应就是设未知数、列方程,这其实只是一种通过设未知数的方式建立等式的方法,属于方程问题中的等量构造,除了这种方法可以解决方程问题外,其实还有另外一种构造等量关系的方式——比较构造法。
一、 什么叫比较构造法
简单地说,就是通过对题干的描述与理解,找到或构造出两种不同的分配方案,并且比较出其中的差异从而列出等量关系式。
二、 经典例题
【例1】某部门购进15包打印纸和20盒水笔用去625元,若第二次购进同样的打印纸10包和同样的水笔20盒用去550元,则一包打印纸的价格为多少元?
A.10元
B.15元
C.20元
D.25元
答案:B
【解析】
方法一:等量构造法:通过题目可知,在两次购买打印纸盒水笔时,分别给出了购买的数量和最终花费的钱数,由“消费金额=单价×销量”可建立等量

方法二:比较构造法
首先可以根据题干描述的信息列出方案:
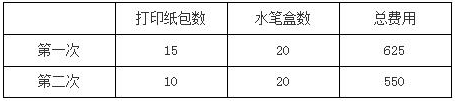
然后去比较两次方案中差异就会发现:第二次比第一次少买了5包打印纸,总费用就少了625-550=75元,故总费用减少75元的原因就是由打印纸数量减少了5包造成的,所以一包打印纸的价格就是75÷5=15元,选B。
【例2】某所中学将三好学生名额分配给若干班级,如果每个班级分3个名额,则多出了5个名额;如果每个班级分4个名额,则少了10个名额。求一共有多少个三好学生名额?
A.38个
B.44个
C.50个
D.56个
答案:C。
【解析】该题是对三好学生名额给出了两种不同的分配方案,可用比较构造进行解决。首先可以根据题干描述的信息列出方案:
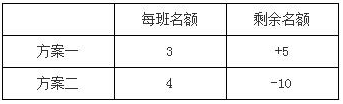
然后去比较两次分配方案的差异就会发现:若每班3个名额时,会剩余5个名额;若每班分4个名额时,除了会将方案一剩余的5个名额分配完,还缺少10个名额。所以,每个班级多分1个名额的话,将会需要5+10=15个名额,即该中学一共15个班级。那么所求为:3×15+5=50个名额,选C。


点击分享此信息:
 相关文章
相关文章


